A Cheat Sheet for Fire and EMS
Actually, it’s not that bad, according to Remle Crowe, a research fellow with NREMT: “Statistics is like a language that helps us understand what our data are trying to tell us,” she said. Better yet, she added, “Statistics can be understood by everyone – not just statisticians, not just PhD students, and not just people who are really good at math.”
We gave Crowe the chance to prove that claim by inviting her to present at ESO’s Wave 2018 Conference. And while 100% of the attendees walked out of the room, it wasn’t until after they were done clapping at the end of her presentation. Highlights included:
Why EMS and the Fire Service Need to Care About Statistics
Statistics have two powerful capabilities that can be useful in EMS and the fire service:
- Detecting when a true difference exists (such as whether your agency’s chest pain protocol is better at detecting STEMIs among male vs. female patients)
- Predicting future values using existing data (such as whether specialized intubation training will make a difference in first-time intubation success rates)
What Sampling Is
When resources are limited, we take a smaller group (sample) and make conclusions about a larger population. (After all, it would be hugely impractical to review, say, every call in the U.S. with a primary impression of stroke for an entire year to assess how often a blood glucose level was documented.) Virtually every survey that makes the headlines is based on sampling.
What Sampling Isn’t
Perfect. Sampling is subject to variation – the idea that if you randomly grab 100 people from a crowd, you’re likely to get a different set of people than if you reached into the same crowd and again grabbed 100 people at random. That’s random normal expected variation. Statistics can help determine whether the differences observed between those two groups are due to the variation in the groups.
Understanding Sample Quality
How representative is your data of the population you’re trying to generalize to? If you’re trying to compare males and females, the group you’re comparing has to be as equal as possible in everything except gender – e.g., the males can’t be concentrated in age between 20 and 30 while the females are concentrated between 40 and 50. The sample also has to be large enough – e.g., a survey of Rhode Island residents over 100 years old wouldn’t require as large a sample as, say, a survey of Californians under 65. Larger populations require larger samples.
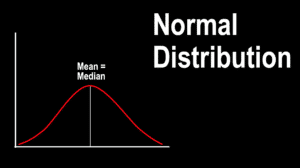
How to Tell Normal Data From Random Variation
To keep things simple, Crowe suggests looking for the familiar bell curve shape. If you see one, and the mean and the median are about equal, you’re probably dealing with normal data. Anything else is probably non-normal data.
What a P-Value Is
There are lots of definitions, but Crowe prefers this one:
Assuming that there is no true difference, the probability of observing what you saw, or something more extreme.
P-values of less than .05 are strongly suggestive that your findings are due to something that actually exists, rather than pure randomness.
What a P-Value Isn’t
A p-value (even a low one) does not indicate is how precise the data is, nor does a low p-value equal causation.
What a Confidence Interval Is
Confidence interval is a gauge of how variable an estimate is. It’s typically expressed in percentage, e.g., a survey finding of 80% compliance with a new protocol, with 95% confidence that the true compliance rate lies between 72% and 88%. Confidence intervals, and precision in general, are affected by sample size. A larger sample can result in a narrower confidence interval – meaning greater precision.